The Charge Distribution method
1. Introduction
The Charge Distribution method (CD or CHARDI), introduced by Hoppe et al. (1989), is the most recent development of the classical theory of the bond strength (Pauling, 1929) and differs from the Bond Valence (BV) approach (e.g. Brown, 1978) in exploiting the true bond distances in a self-consistent computation, instead of employing empirical curves requiring empirical parameters. It applies to structures that can be described in the framework of a Madelung approach, i.e. where the atoms are described as dimensionless point charges forming coordination polyhedra. The atoms at the centre of the polyhedra are indicated as PC-atoms, those at the corners (vertices) of the polyhedra as V-atoms. Electropositive (« cations ») and electronegative (« anions ») are alternatively assigned the role of PC-atoms and V-atoms and both descriptions are used to analyse the structure.
The core of the method consists in the computation of ECoN – Effective Coordination Number (Hoppe, 1979) around a PC-atom which is coordinated by V-atoms. ECoN is a real (non-integer) number which takes into account not only the number of V-atoms around a given PC-atom, but also their weight in terms of relative distances. For uniform coordination polyhedra (all the PC-V distances identical) ECoN reduces to the classical coordination number.
The formal oxidation number of each PC-atom is used as weight for the fractional contribution given by each type of V-atoms to ECoN of that PC-atom. Then, the sums around PC and around V gives what we call « charges« . How to read these « charges » is described below.
CHARDI in practice works on an ionic-analogue of the real crystal: all the atoms in the structure are formally replaced by point charges. The method however does not make reference to an ionic model of bonding, but is applies equally well to covalent bonds and to hydrogen bonds. It requires, however, that the compound be a normal valence compound, (Parthe 1996)1: in other words, a compound containing only bonds of type between electropositive and electronegative atoms, without metallic or molecular bonds (ECoN does not suffer this limitation).
1Rigorously speaking, normal valence compounds defined according to Parthe (1996) do not include cations with lone-pairs. This condition is not influential to apply CHARDI, and thus we include them in a slightly enlarged definition.
2. Notation
PC(ij) = polyhedron-centring atomic site; i = atomic species, j = crystallographic type
V(rs) = corner (vertex) atomic site; r = atomic species, s = crystallographic type
h(ij), h(rs): multiplicities of the Wyckoff positions for PC(ij) and V(rs) respectively
q(ij), q(rs): formal oxidation numbers of PC(ij) and V(rs) respectively
Q(ij), Q(rs): computed « charges » of PC(ij) and V(rs) respectively
d(ij→rs)L: the L-th distance between P(ij) and V(rs), ordered increasingly
nd(ij→r): weighted mean distance between PC(ij) and V(r), after convergence at the n-th cycle of calculation
w(ij→rs)L: bond weight of the d(ij→rs)L distance PC(ij) and V(rs)
3. Calculation procedure.
The complete procedure is described in detail in the articles quoted below. Here we give only the main principles.
3.1 Definition of the coordination polyhedron
To each bond distance a Fictive Ionic Radii FIR(ij→rs)L (Hoppe, 1979) is assigned:
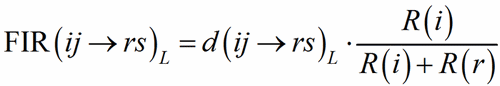 (1)
(1)
where R(i) and R(r) are the ionic radii of PC(ij) and V(rs). In case of uniform coordination polyhedra, all the FIR(ij→rs)L are identical and the deviation from the ionic radius may be read as a measure of the departure from the pure ionic character of the bond. For non-uniform polyhedra, instead, the concept of ionic radius is less well defined; accordingly, a different Fictive Ionic Radius is assigned to each bond, which is then used to compute a weighted average, called the MEan Fictive Ionic Radius (MEFIR). Concretely, an atom at the centre of a uniform polyhedron can be described as a sphere whose dimension, FIR, is directly related to the ionic radius, R(i). For non-uniform polyhedra, instead, the ionic radius shows a dependence on the direction, which leads to a polyhedral shape for the atomic basins. The computation of MEFIR corresponds to assigning to the atom a spherical basin whose radius is a weighted average of the ionic radius for each direction. MEFIR is calculated through a convergent iterative process:
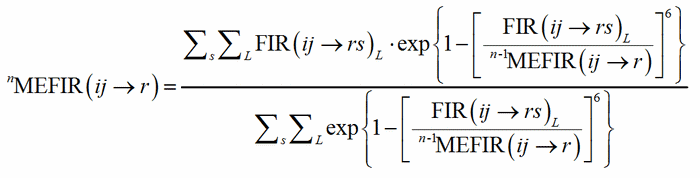 (2)
(2)
where n is the number of iterations and where the starting value, 0MEFIR(ij→r), is simply FIR(ij→rs)1. The exponential term is responsible for the asymptotic decrease of the contribution of each FIR with the increasing of the bond distance.
The classical definition of the coordination number of an atom becomes less and less satisfactory with the distribution of bond distances over a large interval, from uniform polyhedra to cavities which can hardly be recognized as polyhedra, like in the typical example of alkaline metals showing a very irregular coordination. The generalisation of the concept of coordination number as a function of the weighted average of bond distances was called the Effective Coordination Number, ECoN (Hoppe, 1979). A weighted mean distance nd(ij→r) is computed through a convergent iterative process similar to that used to compute MEFIR:
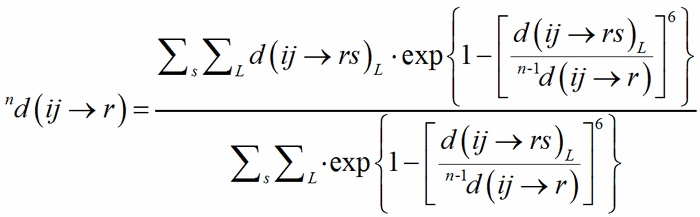 (3)
(3)
with 0d(ij→r) = d(ij→rs)1. The shortest PC-V distance in each polyhedron is used as normalising parameter at the zero-th stage of the iteration, to be replaced by the weighted average until convergence is reached. This exponential term is a measure of the bond strength and have been called the bond weight (Nespolo et al., 2001) nw(ij→rs):
 (4)
(4)
The sum over the bond weights gives the ECoN(ij→r):
 (5)
(5)
In structure built only on homoligand polyhedra (only one type of V-atom), r = 1 and a unique ECoN(ij) for each polyhedron is obtained from Eq. (5).
ECoN, as a generalisation of the classical coordination number, is a real number that has to become equal to the integer coordination number for uniform polyhedra. This is the condition imposed to obtain the contraction parameter 6 in the definition of the weight w(ij→rs) and well as of MEFIR. It was in fact obtained by finding the highest value giving an ECoN equal to the number of first neighbours in the structure of simple metals, where a clear separation between a first and a second coordination sphere exists (Hoppe, 1979). For the very special case of hydrogen bonds, where the ratio of two short distances (donor-H and H-acceptor) with a high relative gap made the weight w(ij→rs) for the second bond negligible, a revised contraction parameter of 1.6 has been introduced (Nespolo et al., 2001).
Eq. (3) and (4) can be rewritten in terms of FIR and MEFIR:
 (6)
(6)
so that the bond weight too can be rewritten in terms of FIR and MEFIR. The advantage is that each heteroligand polyhedron is divided into homoligand subpolyhedra, treated independently, which is of paramount importance to distribute the charge of different V-atoms among the PC-atoms with which they form a chemical bond (Nespolo, 2016).
3.2 Calculation of the Charge Distribution
ECoN(ij→r) is distributed among all the bonds around the PC-atom defining a homoligand subpolyhedron, obtaining in this way the contribution by each V-atom to ECoN itself.
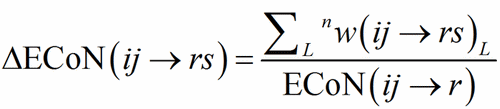 (7)
(7)
In a correctly refined and well-balanced structure, the distribution of ECoN among the PC-V bonds should sum up to some expected value for both PC(ij) and V(rs). As expected value, the formal charge q(ij) is used as a scaling parameter applied to ?ECoN:
 (8)
(8)
Summing the Δq(ij→rs) on the PC-atoms about a V-atom, one should obtain the expected « charge » of the V-atom itself:
The ratio of the multiplicities of the respective Wyckoff positions, h(ij)/h(rs), is introduced to avoid counting multiple contributions when a bond connects atoms on Wyckoff positions with different multiplicities.
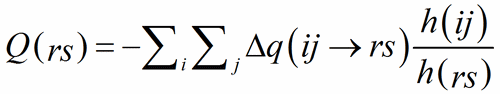 (9)
(9)
A similar distribution is repeated the other way round and summed up on the V-atoms about a PC-atom. This time, however, instead of using q(rs) as scaling parameter, in a perfectly symmetrical way, the ratio q(rs)/Q(rs) for the V(rs) bonded to PC(ij) is used:
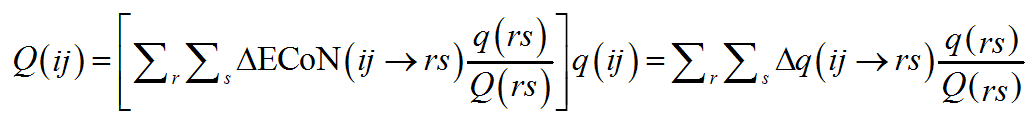 (10)
(10)
As an overall measure of the agreement between q and Q for the whole sets of PC-atoms and of V-atoms, the mean absolute percentage deviation (MAPD) is used:
 (11)
(11)
In the case of homoligand polyhedra (r = 1), every PC-atom distributes its charge to all the V-atoms bonded to it, in an inverse proportion to the bond length. In a heteroligand polyhedra (r > 1), each PC-atom distributes a fraction of its charge to each homoligand subpolyhedron. This fraction depends on the relative distances: V-atoms closer to the PC-atom receive a larger fraction than V-atoms farther from it. The problem is how to define this fraction. This is straightforward for structures which are built by homoligand polyhedra in one of the two possible descriptions (cation-centred or anion-centred), while it requires a convergence algorithm when a structure is built by heteroligand polyhedra in both descriptions.
3.2.1. Structures built by homoligand polyhedra in one description
If a structure contains only one chemical species of cations or of anions, the calculation is straightforward. The single-type of atom (cation or anion) is first assigned to V-atoms and the computation described above is performed. Next, the fraction of Q(ij) coming from each V-atom is calculated by a simple modification of Eq. (10):
 (12)
(12)
The summation is here over j, i.e. the crystallographic type of PC-atom, instead than r and s. The result is thus the fraction of the formal charge that each V-atom (of chemical species r and crystallographic type s) shares with the i-th chemical species of PC-atom. The role of PC-atoms and V-atoms is then exchanged so that Eq. (12) gives in the next step ΔQ(ij→r), i.e. the fraction that each PC-atom (V-atom in the previous step) shares with each chemical species of V-atom (PC-atom in the previous step):
![]() (13)
(13)
with the exchange r→i, j→s, i→r. ΔQ(ij→r) is then used instead of q(ij) in Eq. (10), which is replaced by Eq (14):
 (14)
(14)
Clearly, if r = 1, Eq. (14) reduces to Eq. (10).
3.2.2 Structures built by heteroligand polyhedra in both descriptions
When a structure contains heteroligand polyhedra in both descriptions, we miss the starting point to compute Eq. (12). The problem is solved with an iterative procedure in which the starting value of ΔQ(ij→r) in Eq. (13) is assigned as a function of ECoN(ij→r)/ECoN(ij):
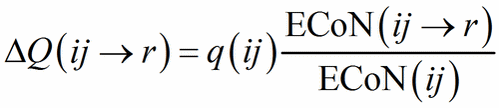 (13′)
(13′)
Eq. (13′) corresponds to Pauling’s definition of bond strength (s = Q/N, N being the classical, integer coordination number) applied to each sub-polyhedron. From the second step Eq. (12) and (13) can be used directly and the role of PC and V-atoms is swapped back and forth between cations and anions until the same values of ΔQ(ij→r) are obtained in each description, meaning that convergence has been obtained.
4. Interpretation of the results
If q(rs)/Q(rs) = 1 for each r and s, then the bracket in equation (10) goes to 1 (it becomes the sum of the fractions of ECoN about each PC-atom) and thus Q(ij) = q(ij). This shows that in a structure correctly solved and perfectly valence-balanced the distribution of ECoN scaled by the formal charges gives back these charges.e other hand, when a structure has developed some structural tensions, its V-atoms may not be perfectly balanced but the distribution of this unbalance, measured by the ratio q(rs)/Q(rs), should give back the expected formal charges on the PC-atoms, otherwise the whole set of coordination polyhedra would be unbalanced and the structure would be unstable. In other words, CHARDI possesses an internal criterion to evaluate the quality of its analysis: the ratio q(ij)/Q(ij) for the PC-atoms. When this ratio is reasonably close to 1 for all the PC atoms, then the analysis of the connectivity can be approached by the study of the Q(rs), which diverge from q(rs) proportionally to the structural strains inside the structure. One speaks of over-under-bonding (OUB) effect (Nespolo et al., 1999, 2001). Quite obviously, in the trivial case of a structure containing only one type of V-atom there is nothing to distribute, Q(rs) is identical to q(rs) and the CHARDI analysis simply does not give any information.
Reasons for q(ij)/Q(ij) significantly deviating from 1 can be:
- the refined structure model is inadequate including overlooked (light) atoms and disorder
- wrong assignment of oxidation numbers, including the case of sites with isomorphous substitutions
- presence of polyions, which are not accounted for by the Madelung-type description of the structure adopted Chardi approach;
- the coordination of one or more PC-atoms is so distorted that the polyhedral description is too approximate.
When instead q(ij)/Q(ij) is reasonably close to 1, Q(rs),ECoN(ij→r) and, with reference to each bond, w(ij→r)L, are suitable parameters to investigate structural changes, e.g. as a function of composition, temperature and pressure. Therefore, differently from the Bond Valence method, in the Chardi approach the computed « charges » (Q) of the PC-atoms and of the V-atoms convey different information. The analysis of the structural details on the basis of the strength of each bond (termed « bond valence » in the homonymous method and « bond weight » in Chardi) is meaningful only when the structure is correctly refined and the empirical method itself is applicable. The CD method has in (q/Q)PC ratio precisely this kind of criterion (Nespolo et al., 2001).
The FORTRAN program
CHARDI2015 is a Fortran program that computes the Charge Distribution in non-molecular structures. It uses a graphical user interface (ChardiGUI) which accepts in input CIF files. Details are described in the « readme » text provided with the installer.
Revision history
- April 28, 2017: CIF parser updated to take into account the new CIF data name (see note below). CHARDI2015 build is not changed but we suggest to reinstall it to avoid problems with the CIF name described below
- Build 21: released February 9, 2016: fixed a bug for structures containing atoms with non-integer charges
- Build 20: released February 8, 2016: fixed a bug for structures containing hydrogen bonds
- Build 19: released January 15, 2016: fixed a bug for structures containing hydrogen atoms
- Build 18: released November 17, 2015
=== Download CHADI2015 from this link (9 Mo) ===
Warning!
You may need to turn off your antivirus during installation, and add the install directory in the list of exceptions of your antivirus!
You may need to install Visual C++ Redistributable for Visual Studio 2015 to run CHARDI2015. You can download it from Microsoft website.
The software writes the output in a text file. If you install the software in a system folder like « Program Files (X86) » it is recommanded not to put your input (CIF) file in the same folder but in user folder or partition instead.
Note on the CIF name
The CIF data name
_atom_site_symmetry_multiplicity
has now been replaced with two new names
_atom_site_site_symmetry_multiplicity
_atom_site_site_symmetry_order
to avoid confusions between the the order of the space-group site symmetry and the multiplicity. Some refinement programs still use the old name, other print out the new names.
The CIF parser used by CHARDI2015 before Apri 28, 2017, recognized the old CIF name but not the new one. The new version of the CIF parser recognize both names.
If you have installed CHARDI2015 before April 28, 2017, we suggest you resintall it even if the build is the same. The Setup program will install the new CIF parser.
References
- Brown, I. D. (1978) Bond valences – a simple structural model for inorganic chemistry. Chem. Soc. Rev. 7, 359-376.
- Eon, J.-G., Nespolo, M. (2015). Charge distribution as a tool to investigate structural details. III. Extension to description in term of anion-centred polyhedra. Acta Crystallographica B71, 34-47.
 Electronic reprint (430 Ko).
Electronic reprint (430 Ko). - Hoppe, R. (1979). Effective coordination numbers (ECoN) and mean fictive ionic radii (MEFIR). Z. Kristallogr., 150, 23-52.
- Hoppe, R., Voigt, S., Glaum, H., Kissel, J., Muller, H. P., Bernet, K. (1989). A new route to charge distributions in ionic solids. J. Less-Comm. Met., 156, 105-122.
- Nespolo, M., Ferraris, G., Ohashi, H. (1999). Charge Distribution as a tool to investigate structural details: meaning and application to pyroxenes. Acta Crystallographica B55, 902-916.
- Nespolo, M., Ferraris, G., Ivaldi, G., Hoppe, R. (2001). Charge Distribution as a tool to investigate structural details. II. Extension to hydrogen bonds, distorted and hetero-ligand polyhedra. Acta Crystallographica B57, 652-664.
 Electronic reprint (363 Ko)
Electronic reprint (363 Ko) - Nespolo, M., (2016). Charge Distribution as a tool to investigate structural details. IV. A new route to heteroligand polyhedra. Acta Crystallographica B72, 51-66.
 Electronic reprint (792 Ko)
Electronic reprint (792 Ko) - Nespolo, M., Guillot, B. CHARDI2015: Charge Distribution analysis of non-molecular structures. J. Appl. Crystallogr., 49, 317-321.
 Electronic reprint (636 Ko)
Electronic reprint (636 Ko) - Parthe E. (1996). Elements of Inorganic Structural Chemistry, second edition. Petit-Lancy: K. Sutter Parthe
- Pauling, L. (1929). The principles determining the structure of complex ionic crystals. J. Am. Chem. Soc., 51, 1010-1026.