PTST98

PTST98 (PolyType STacking) is a simple program that computes the Periodic Intensity Distribution (PID) function of mica polytypes.

Mica polytypes are built by stacking a unit layer (commonly indicated as «M layer» through one or more generating operations: these are local symmetry operations (space-groupoid operations) valid in the crystal subspace corresponding to a pair of layers, but not valid in the whole crystal space. Successive layers are differently oriented, and the relative rotations about c * are n x 60° ( n = 0-5). These rotations are nothing else than a description of the stacking mode in micas: they are not generating operations from either the geometrical or the crystal-growth viewpoint.

The number of polytypes increases dramatically with the number of layers ( Mogami et al. , 1978 ; McLarnan, 1981 ) and the identification of the stacking sequence of a long-period mica polytype requires thus an indirect procedure which exploits the periodicity in reciprocal space. This simplified procedure was introduced by Takeda (1967) under of the name of Periodic Intensity Distribution (PID). The PID is an approximant of the Fourier transform of the stacking sequence that can be obtained in a simple way from the diffraction intensities.

The Fourier transform of a polytype ( G^N, where N is the number of layers) is given by the Fourier transform of the stacking sequence, modulated by the Fourier transform of the layer ( G_j ):

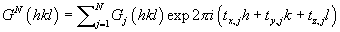
where t_x,j, t_y,j, t_z,j are the ( x, y, z ) components of the stacking vector relating the j -th and the ( j +1)-th layers. When the shifts between the building layers are rational and the rotations belong to the symmetry of the layer(s), their Fourier transform ( G_j ), which is a continuous function in the direction of lacking periodicity, can be extracted from the expression of the structure factor G^N. G^N takes thus the simple form of the product of the layer transform and of the stacking sequence transform. The second term expresses the periodicity in reciprocal space appearing when a structure is built by translation of subunits. This is the case of polytypes of binary compounds like SiC and ZnS.

In micas, the M layers are instead related by rotations belonging not to the layer symmetry but to the idealised symmetry of the O _b plane (with the obvious exception of the 1 M polytype) and the same simplification is in principle not possible. However the Fourier transform of the M layer in the six possible orientations is almost unmodified in a subspace of the reciprocal space ( Takeda, 1967 ). By removing the modulating effect of the layer, the approximated Fourier transform of the stacking sequence is obtained. This is known as Periodic Intensity Distribution ( PID ) function. Comparison of calculated and observed PID values along lattice rows parallel to c * with k ≠ 3 n ( non-family rows: Ďurovič et al. , 1984 ; X rows: Nespolo et al. , 2000 ) is in principle sufficient to identify any mica polytype ( Takeda and Ross, 1995 ; Nespolo et al. 1999 ).

The PTST98 program uses the RTW rotational symbols ( Ross et al. , 1966 ) of a stacking candidate to compute the PID function. Instructions and examples are included in the downloadable ZIP file.

Fichier Windows : PTST.zip (379 Ko)